Spring, 2000, Assignment
| Go to assignment # |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12
|
| Due on Monday |
02/14 |
02/21 |
02/28 |
03/06 |
03/13 |
03/20 |
04/03 |
04/10 |
04/17 |
04/24 |
05/01 |
05/08 |
| Chapter |
22 |
23 |
23, 24 |
25 |
26 |
27, 28 |
29 |
30 |
31 |
31 |
33 |
33 |
I will almost always have hints posted on the web beginning a week
before the assignment is due. The day before the problem session I
will try to post answers in the same location. I will frequently post
solutions after the problem session is over.
In general, I have chosen problems like the more difficult ones in the
chapter. It may be helpful to work a few of the simpler problems
first, especially if you have trouble getting started on one of the
assigned problems. If you have difficulty, see me in Sharp Lab 264,
call x2013, or send EMail to
mvb@udel.edu,
preferably before turning the set in. It is as important to know why
incorrect attempts do not work as it is to know what the correct
solutions are. Please feel free to talk to me at any time either in
person, by phone, or by E-MAIL.
The problems will be graded for the existence of diagrams, the use of
units, and correct vector notation. Otherwise, a reasonable attempt
will get full credit whether it is right or wrong. Since the problems
are graded for technique and not for correctness, you can work with
each other on the assignments. You should do so. You may also consult
others outside the class, but I strongly advise against looking at
their solutions before attempting the problems yourself. You must
write up your own final copy, unless I have stated otherwise (no
Xeroxes!).
Many of these problems are adapted from a book by Tipler, because I
already have reliable answers and solutions for those problems.
Similar problems appear in our text. I am also modifying some of the
problems from the text so that they fit better with the other assigned
problems. Whenever the assigned problem is very similar to one in the
text, the assignment includes the statement "compare HRW # ...." If
an assigned problem is nearly identical to one in the text, the
assignment will say "see HRW # ...."
1. Due in recitation 02/14
Go to Hints
Go to Answers
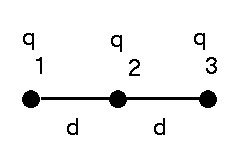
Chapter 22. Electric Charge:
1. (HRW p. 551 # 8) In the figure on the right (HRW
figure 22-21), three charged particles lie on a straight line and are
separated by a distance d. Charges q1 and
q2 are held fixed [by external forces]. Charge
q3 is free to move but happens to be in
equilibrium (no net electrostatic force acts on it). Find
q1 in terms of q2.
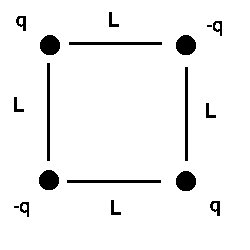 2. Four charges,
each of magnitude q, are at the corners of a square of side
L. The two charges at one pair of opposite corners are
positive, and the other two charges are negative. Find the force
exerted on either of the negative charges by the three remaining
charges. See figure to the right.
2. Four charges,
each of magnitude q, are at the corners of a square of side
L. The two charges at one pair of opposite corners are
positive, and the other two charges are negative. Find the force
exerted on either of the negative charges by the three remaining
charges. See figure to the right.
3. (See HRW p. 551 #18 and p. 553 #41). A certain
charge Q is divided into two parts alpha Q and
(1 - alpha) Q, which are then separated by a certain
distance. What must alpha be in order to maximize the
electrostatic repulsion between the two charges? Draw a graph of the
electrostatic force F as a function of alpha and
verify the correctness of your answer.
 4. (HRW p. 551 #20). In the figure on the right, two
tiny conducting balls of identical mass m and identical
charge q hang in equilibrium from nonconducting threads of
length L. Assume that theta is so small that
tan(theta) can be replaced by its approximate equal
sin(theta) [both are in fact essentially equal to
theta]. (a) Show that, for equilibrium,
4. (HRW p. 551 #20). In the figure on the right, two
tiny conducting balls of identical mass m and identical
charge q hang in equilibrium from nonconducting threads of
length L. Assume that theta is so small that
tan(theta) can be replaced by its approximate equal
sin(theta) [both are in fact essentially equal to
theta]. (a) Show that, for equilibrium,
x = [q2 L / ( 2 pi epsilon0 m g ]1/3
where x is the separation between the balls. (b) If
L=120 cm , m=10 g, and
x=5.0 cm, what is q?
2. Due in recitation 02/21
Go to Hints
Go to Answers
Chapter 23. Electric Fields:
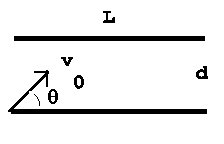 5. (Compare HRW p. 577
# 57) Two charged plates of length L are placed a distance
d apart as shown in the figure to the right. An electron is
injected between the plates, just clearing the lower plate as it
enters. It feels a constant electric field E pointed straight
upward due to the charges on the plates. If the electron's initial
velocity is v0 at an angle theta with respect to the lower
plate, for what values of theta will it not hit the upper plate? If
it clears the upper plate, how far does it get before hitting the
lower plate?
5. (Compare HRW p. 577
# 57) Two charged plates of length L are placed a distance
d apart as shown in the figure to the right. An electron is
injected between the plates, just clearing the lower plate as it
enters. It feels a constant electric field E pointed straight
upward due to the charges on the plates. If the electron's initial
velocity is v0 at an angle theta with respect to the lower
plate, for what values of theta will it not hit the upper plate? If
it clears the upper plate, how far does it get before hitting the
lower plate?

6. (Compare HRW p. 575 #22)
Four charges of equal magnitude are arranged at the corners of a
square of side L as shown in the figure to the right. Show
that the electric field at the midpoint of one of the sides of the
square is directed along that side, points toward the negative charge,
and has a magnitude E given by
E = [1/4 pi epsilon0 ] [8 q / L2 ] [ 1 - 51/2 / 25]
7. A water molecule has its
oxygen atom at the origin, one hydrogen nucleus at
x = 0.077 nanometer, y = 0.058 nm, and the
other hydrogen nucleus at x = - 0.077 nm,
y = 0.058 nm. If the electrons from the hydrogen atoms
are transferred completely to the oxygen atom so that it has a charge
of -2e, what is the dipole moment of the water molecule?
[This characterization of the chemical bonds of water as being totally
ionic overestimates the dipole moment of a water molecule].
8. A positive point charge
+Q is at the origin. A dipole of moment p is a
distance r away from the charge and points in the radial
direction, as shown in the diagram to the right.

(a) Show that the force exerted by the electric field of the point
charge on the dipole is attractive and has a magnitude of
approximately
F = 2 Q p / (4 pi epsilon0 r3 )
(b) Now assume that the dipole is centered at the origin and that the
point charge Q is a distance r away along the line
of the dipole. From your result in part (a) and Newton's Third Law,
show that the magnitude of the electric field of the dipole along the
line of the dipole a distance r away is approximately
E = 2 p / (4 pi epsilon0 r3 )
9. (HRW p. 575 # 26) Electric Quadrupole
. The figure shows an electric quadrupole. It consists of two
dipoles with dipole moments that are equal in magnitude but opposite
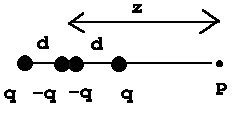 in direction. Show that the value of the magnitude of the electric
field E on the axis of the quadrupole for points a distance
z from its center (assume z >> d) is given by
in direction. Show that the value of the magnitude of the electric
field E on the axis of the quadrupole for points a distance
z from its center (assume z >> d) is given by
E = 3 Q / ( 4 pi epsilon0 z4 )
in which Q (=2 q d2) is known as the quadrupole
moment of the charge distribution. [This is not the only way to
get a quadrupole moment.]
10. (Compare HRW p. 576 #33) (a)
A thin, nonconducting rod carries a charge of constant linear charge
density lambda and lies on the x-axis from x =
0 to x = a. Show that the y-component of the
electric field at any point on the y-axis is given by
Ey = [ lambda a / ( 4 pi epsilon0 y) ]
( y2 + a2) - 1/2
Go to solution for part (a)
(b) Show that if the rod extends from x = - b to
x = a, the y-component of the electric field at the same
point is given by
Ey = [ lambda a / ( 4 pi epsilon0 y) ]
(y2 + a2) -1/2
+ [ lambda b / ( 4 pi epsilon0 y) ]
(y2 + b2) -1/2
(c) HRW asks for the special case a = b = L/2. Show that in
this case you get
Ey = [ q / ( 2 pi epsilon0 y) ]
( 4 y2 + L2) - 1/2
(d) Show that if and only if a = b the x-component of the electric
field vanishes.
11. A butterfly net is attached to a
ring of radius R, and the ring is held in a plane perpendicular to a
constant electric field of magnitude E. What is the electric flux
PHI=integral [E cos(theta) dA]
through the net? The angle theta is the angle between the
normal to the net and the electric field.
3. Due in recitation 02/28
Go to Hints
Go to Answers
Chapter 23. Electric Fields
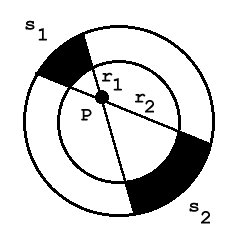 12. A spherical shell
of radius R carries a uniform surface charge density
sigma which you may consider to be positive. The figure to
the right shows a cross-section of the shell. A point P is
in the plane of the cross-section but not at the center. Consider the
two elements of the shell of areas s1 and
s2 shown in the figure at distances
r1 and r2 , respectively, from
point P. (a) Show that the ratio of the charges on these
elements is
Q1 / Q2 = r1 2 / r2 2
(b) Which produces the greater field at point P? (c) What is
the direction of the field at point P due to each element?
What is the direction of the total electric field at point P?
(d) Using the result in part (c), explain how it is possible to use
Gauss's Law to calculate the electric field without taking into
account any charges outside the Gaussian surface, provided that
sufficient symmetry is present. What is the role of the symmetry
requirement?
12. A spherical shell
of radius R carries a uniform surface charge density
sigma which you may consider to be positive. The figure to
the right shows a cross-section of the shell. A point P is
in the plane of the cross-section but not at the center. Consider the
two elements of the shell of areas s1 and
s2 shown in the figure at distances
r1 and r2 , respectively, from
point P. (a) Show that the ratio of the charges on these
elements is
Q1 / Q2 = r1 2 / r2 2
(b) Which produces the greater field at point P? (c) What is
the direction of the field at point P due to each element?
What is the direction of the total electric field at point P?
(d) Using the result in part (c), explain how it is possible to use
Gauss's Law to calculate the electric field without taking into
account any charges outside the Gaussian surface, provided that
sufficient symmetry is present. What is the role of the symmetry
requirement?
13. A disk of radius
R carries a uniform charge density sigma. (a)
Compare the approximation E = sigma / (2 epsilon0
) with the exact expression for the electric field on the axis of
the disk by computing the neglected term as a percentage of sigma
/ (2 epsilon0 ) for distances of x = R / 300 ,
x = R / 150 , and x = R / 10 . (b) At what
distance is the neglected term 1% of sigma / (2
epsilon0 ) ?
 14. (Hint: compare HRW p. 576 #34) In the figure to
the right, two nonconducting rods of length L have charge
q uniformly distributed along their lengths. (a) What is the
linear charge density of each rod? (b) What is the electric field
E due to the left-hand rod at a distance a beyond
its right-hand end? (c) What is the force that one of the rods exerts
on the other? (d) Show that when the distance d between the
rods becomes large compared to the length of the rods, the force tends
toward the expected result q2 / d2.
14. (Hint: compare HRW p. 576 #34) In the figure to
the right, two nonconducting rods of length L have charge
q uniformly distributed along their lengths. (a) What is the
linear charge density of each rod? (b) What is the electric field
E due to the left-hand rod at a distance a beyond
its right-hand end? (c) What is the force that one of the rods exerts
on the other? (d) Show that when the distance d between the
rods becomes large compared to the length of the rods, the force tends
toward the expected result q2 / d2.
Chapter 24: Gauss's Law
15. (HRW p. 599 #51) A point charge +q is
placed at the center of an electrically neutral, spherical conducting
shell with inner radius a and outer radius b. What
charge appears on (a) the inner surface of the shell and (b) the outer
surface of the shell? Find expressions for the net electric field at
a distance r from the center of the shell if (c) r < a
, (d) b > r > a, and r > b. Sketch the field
lines for those three regions. For r > b, what is the net
electric field due to (f) the central point charge and inner surface
charge and (g) the outer surface charge? A point charge -q
is now placed outside the shell. Does this point charge change the
charge distribution on (h) the outer surface and (i) the inner
surface? Sketch the field lines now. (j) Is there an electrostatic
force on the second point charge? (k) Is there a net electrostatic
force on the first point charge? (l) Does this situation violate
Newton's third law?
16. (HRW p. 599 #52). A solid nonconducting sphere of
radius R has a nonuniform charge distribution of rho =
rhos r / R, where rhos is a
constant and r is the distance from the center of the
sphere. Show that (a) the total charge on the sphere is Q = pi
rhos R 3 and (b) the electric field inside
the sphere has a magnitude given by
E = [1 / ( 4 pi epsilon0 ) ] [ Q r2 /
R4 ]
17. (Compare HRW p. 598
#31) An infinitely long nonconducting cylindrical shell of inner
radius a and outer radius b has a uniform volume
charge density rho . Find the electric field everywhere.
18. An infinitely long nonconducting
solid cylinder of radius R has a charge density of B /
r , where r is the distance from the axis of the
cylinder. Find the electric field everywhere.
4. Due in recitation 03/06
Go to Hints
Go to Answers
Chapter 25. Electric Potential:
19. Two positive charges
+ q are on the x-axis at x = + a and x
= - a . (a) Find the potential V(x) as a function of
x for all points on the x-axis. (b) Sketch
V(x) . (c) What is the significance of the minimum of your
plot of V(x) ?
20. Three
equal charges lie in the xy plane. Two are on the
y-axis at y = - a and y = + a , and the
third is on the x axis at x = a . (a) What is the potential
V(x) due to these charge at any point on the x-axis?
(b) Find Ex along the x-axis from the
potential function V(x) . Evaluate your answers to (a) and
(b) at the origin and at x = infinity to see if they yield
the expected results. (c) If a fourth charge of + q is
released at the origin, what is its velocity when it gets very far
away from the other three?
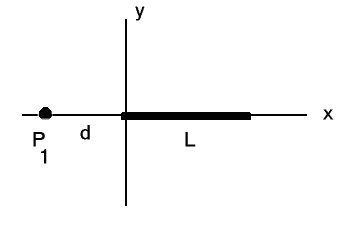
21. (HRW p. 624 #41) The figure shows a plastic rod
of length L and uniform positive charge Q lying on
an x axis. With V = 0 at infinity,
find the electric potential at point P1 on the axis, at
distance d from one end of the rod.
22.
Four equal charges Q are at the corners of a square of side
L. The charges are released one at a time proceeding
clockwise around the square. Each charge is allowed to reach its
final speed a long distance from the square before the next charge is
released. What is the final kinetic energy of (a) the first charge
released, (b) the second charge released, (c) the third charge
released, and (d) the fourth charge released?
23. (Compare HRW p. 624 #
46) The electric potential in a region of space is given by
V(x, y, z) = (2 Volt / m2) x2 + (1 Volt / m2)yz
Find the electric field at all points (x, y, z)
24. Consider two
concentric spherical metal shells of radii a and b
where b > a . The outer shell has a charge Q , but
the inner shell is grounded [it is at the same potential as a point at
infinity]. This means that the inner shell is at zero potential and
implies that electric-field lines leave the outer shell and go to
infinity but that other electric-field lines leave the outer shell and
end on the inner shell. Find the charge on the inner shell.
25.
A nonconducting sphere of radius R has a volume charge
density rho = rho0 r / R , where
rho0 is a constant. (a) Show that the total charge
is Q = pi R3 rho0 . (b) Use Gauss's Law
to find the electric field Er everywhere. (c) From
the electric field, find the electric potential everywhere, assuming
that V = 0 at infinity. (Remember that V is
continuous at r = R .
5. Due in recitation 03/13
Go to Hints
Go to Answers
Chapter 26. Capacitance:
26. (Compare HRW p. 649 #
53, 57) You are asked to construct a parallel-plate, air-gap capacitor
that will store 100 kJ of energy. (a) What minimum volume is required
between the plates of the capacitor? (b) Suppose you have developed a
dielectric that can withstand a maximum electric field
Emax and has a dielectric constant of
kappa. What volume of this dielectric between the plates of
the capacitor is required for it to be able to store 100 kJ of energy?
27. Consider two
parallel-plate capacitors, C1 and C2, that are
connected in parallel. The capacitors are identical except that
C2 has a dielectric inserted between its plates. A voltage
source of V volts is connected across the capacitors to
charge them and is then disconnected. (a) What is the charge on each
capacitor? (b) What is the total stored energy of the capacitors? (c)
The dielectric is removed from C2. What is the final
stored energy of the capacitors? (d) What is the final voltage across
the two capacitors?
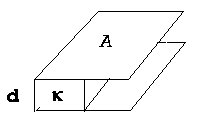 28. (Compare HRW p. 650 #
63) A parallel-plate capacitor of area A and separation
d is charged to a potential difference V and is then
removed from the charging source. A dielectric slab of constant
kappa, thickness d, and area A/2 is
inserted along one edge of the capacitor as shown in the figure. Let
sigma1 be the free charge density at the
conductor-dielectric surface and sigma2 be the
free charge density at the conductor-air surface. (a) Why must the
electric field have the same value inside the dielectric as in the
free space between the plates? (b) Show that
sigma1 = kappa sigma2.
(c) Show that the new capacitance is
28. (Compare HRW p. 650 #
63) A parallel-plate capacitor of area A and separation
d is charged to a potential difference V and is then
removed from the charging source. A dielectric slab of constant
kappa, thickness d, and area A/2 is
inserted along one edge of the capacitor as shown in the figure. Let
sigma1 be the free charge density at the
conductor-dielectric surface and sigma2 be the
free charge density at the conductor-air surface. (a) Why must the
electric field have the same value inside the dielectric as in the
free space between the plates? (b) Show that
sigma1 = kappa sigma2.
(c) Show that the new capacitance is
C = ( kappa + 1 ) epsilon0 A / ( 2 d )
and that the new potential difference is
2 V / ( kappa + 1 )
29. HRW p. 650 # 68: The space between two
concentric conducting spherical shells of radii b and
a (where b > a) is filled with a
substance of dielectric constant kappa. A potential
difference V exists between the inner and outer shells.
Determine (a) the capacitance of the device, (b) the free charge
q on the inner shell, and (c) the charge q' induced
along the surface of the inner shell.
6. Due in recitation 03/20
Go to Hints
Go to Answers
Chapter 27. Current and Resistance:
30. The wires in a house
must be large enough in diameter so that they do not get hot enough to
start a fire. Suppose a certain wire is to carry a current of 20 A,
and it is determined that the joule heating of the wire should not
exceed 2 W/m. What diameter must a copper wire have to be "safe" for
this current?
31. HRW p. 672 #59: A linear accelerator produces a
pulsed beam of electrons. The pulse current is 0.50 A, and the pulse
duration is 0.10 microsecond. (a) How many electrons are accelerated
per pulse? (b) What is the average current for a machine operating at
500 pulses/s? (c) If the electrons are accelerated to an energy of 50
MeV, what are the average and peak powers of the accelerator?
32. HRW p. 671 #41: A resistor has the shape of a
truncated right-circular cone (see figure 27-25 in text). The end
radii are a and b, and the altitude is L.
If the taper is small, we may assume that the current density is
uniform across any cross section. (a) Calculate the resistance of
this object. (b) Show that your answer reduces to
rho L / A for the special case of zero taper
(that is, for a = b).
Chapter 28. Circuits:
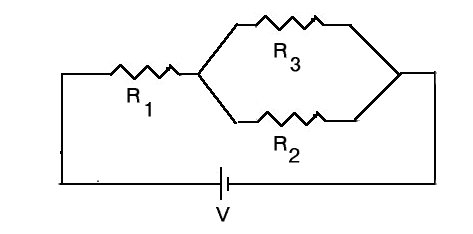 33. A resistor of size R1 is
placed in series with a parallel combination of resistors
R2 and R3. A battery of
voltage V is connected across the entire system, as shown in
the diagram. Find the effective resistance of the system, the voltage
across each resistor, the current through each resistor, and the
current through the battery. [When you get the correct answers, keep
them for use in the assignment on AC circuits.]
33. A resistor of size R1 is
placed in series with a parallel combination of resistors
R2 and R3. A battery of
voltage V is connected across the entire system, as shown in
the diagram. Find the effective resistance of the system, the voltage
across each resistor, the current through each resistor, and the
current through the battery. [When you get the correct answers, keep
them for use in the assignment on AC circuits.]
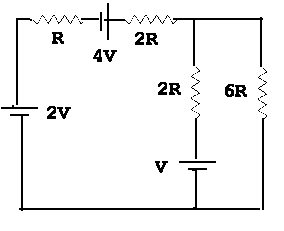 34. For the circuit shown
in the figure, find (a) the current in each resistor, (b) the power
supplied by each EMF, and (c) the power dissipated in each
resistor. (d) Is energy conservation obeyed?
34. For the circuit shown
in the figure, find (a) the current in each resistor, (b) the power
supplied by each EMF, and (c) the power dissipated in each
resistor. (d) Is energy conservation obeyed?
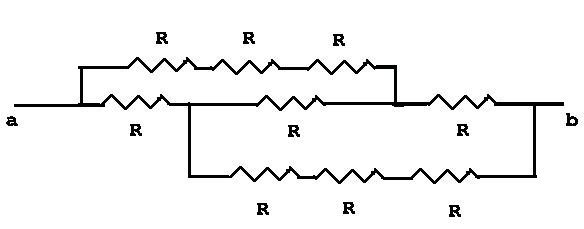 35. Nine resistors of
resistance R are connected as shown in the figure, and a
potential difference V is applied between points a
and b. What is the equivalent resistance of this network? (b)
Find the current in each of the nine resistors.
35. Nine resistors of
resistance R are connected as shown in the figure, and a
potential difference V is applied between points a
and b. What is the equivalent resistance of this network? (b)
Find the current in each of the nine resistors.
 36. Find the current through each of the elements in
the diagram to the right. The use of a symbolic-algebra computer
program is recommended. [When you have correct answers, keep them for
use in the chapter on AC circuits.]
36. Find the current through each of the elements in
the diagram to the right. The use of a symbolic-algebra computer
program is recommended. [When you have correct answers, keep them for
use in the chapter on AC circuits.]
7. Due in recitation 04/03
Go to Hints
Go to Answers
Chapter 29. Magnetic Fields:
37. HRW p. 725 #55: Figure 29-46 in the text shows a rectangular,
20 turn coil of wire, 10 cm by 5.0 cm. It carries a current of 0.10
A and is hinged along one side. It is mounted in the xy
plane, at an angle of 30o to the direction of a uniform
magnetic field of 0.50 T. Find the magnitude and direction of the
torque acting on the coil about the hinge line.
38. A particle of charge
q and mass M moves in a circle of radius r
and with angular velocity omega. (a) Show that the average
current is
I = q omega / (2 pi ) and
that the magnetic moment has the magnitude
mu = (1/2) q omega r2.
(b) Show that the angular momentum of this particle has the magnitude
L = M r2 omega and that the
magnetic moment and angular momentum vectors are related by
mu = [q/(2M)]L.
39.
A current-carrying wire is bent into a semicircular loop of radius
R, which lies in the xy plane. There is a uniform
magnetic field
B = B 1z
perpendicular to the plane of the loop. Show that the force acting on
the loop is
F = 2 I R B 1y.
40. A nonconducting rod
of mass M and length l has a uniform charge per unit
length lambda and rotates with angular velocity
omega about an axis through one end and perpendicular to the
rod. (a) Consider a small segment of the rod of length dx and
charge dq = lambda dx at a distance x
from the pivot. Show that the magnetic moment of this segment is
(1/2) lambda omega x2 dx. (b)
Integrate your result to show that the total magnetic moment of the
rod is
mu = (1/6) lambda omega l3
(c) Show that the magnetic moment mu and angular
momentum L are related by
mu = [(Q/(2M)] L,
where Q is the total charge on the rod.
8. Due in recitation 04/10
Go to Hints
Go to Answers
Go to Solutions
Chapter 30: Magnetic Fields Due to Currents
41: HRW p. 748 # 45 [reworded without change of
content]. Figure 30-61 shows an approximation to the magnetic field
in a region, and an arrow representing a path through that
region. Show that the uniform magnetic field B cannot
drop abruptly to zero as one moves along a path perpendicular to
B, as shown at point a on the figure.
(Hint: Apply Ampere's law to the rectangular path shown by
the dashed lines.) In actual magnets "fringing" of the magnetic field
lines always occurs, which means that B approaches zero in
a gradual manner. Modify the field lines in the figure to indicate a
more realistic set of lines.
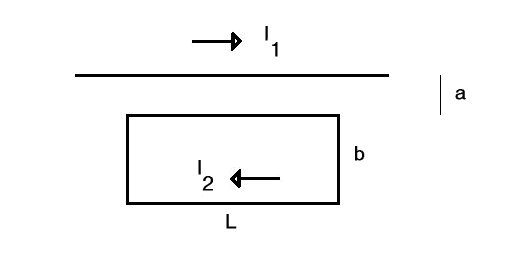
42: HRW p. 747 # 38:
In the figure to the right (HRW figure 30-55), the long straight wire
carries a current of 30 A and the rectangular loop carries a current
of 20 A. Calculate the resultant force acting on the loop. Assume
that the distance a = 1.0 cm,
b = 8.0 cm, and
L = 30 cm.
43: HRW p. 749 #50. Figure 30-64 of the text shows a
cross section of a long cylindrical conductor of radius a
containing a long cylindrical hole of radius b. The axes of
the cylinder and hole are parallel and are a distance d
apart; a current i is uniformly distributed in the conductor
outside the hole. (a) Use superposition to show that the magnetic
field at the center of the hole is
mu0 i d
B = ------------------------
2 pi (a2 - b2)
(b) Discuss the two special cases b = 0 and
d = 0. (c) Use Ampere's Law to show that the
magnetic field in the hole is uniform.
(Hint: Regard the cylindrical hole as filled with two equal
currents moving in opposite directions, thus canceling each other.
Assume that each of these currents has the same current density as
that in the actual conductor. Then superimpose the fields due to two
complete cylinders of current, of radii a and b,
each cylinder having the same current density.)
44. A solenoid has n turns per unit length
and radius R and carries a current I. Its axis is
along the x axis with one end at x = -L/2
and the other end at x = +L/2, where L is
the total length of the solenoid. Show that the magnetic field
B at a point on the axis outside the solenoid is given by
B = (1/2) mu0 n l (cos theta1 - cos theta2)
where
x + (1/2) L
cos theta1 = -------------------------
[ R2 + (x + L/2)2 ]1/2
and
x - (1/2) L
cos theta2 = -------------------------
[ R2 + (x - L/2)2 ]1/2
45. In Problem 44, a formula for the magnetic field
along the axis of a solenoid is given. For x >> L
and L > R, the angles theta1 and
theta2 in that problem are very small, so that the
small angle approximation
cos theta = 1 - theta2 / 2
is valid. (a) Draw a diagram and show that
R
tan (theta1) = ------
x + L/2
and
R
tan (theta2) = -------
x - L/2
(b) Show that the magnetic field at a point far from either end of the
solenoid can be written
mu0 qm qm
B = ---- [ -- - -- ]
2 pi r12 r22
where r1 = x - L/2 is the distance to
the near end of the solenoid,
r2 = x + L/2 is the distance to the far
end, and qm = n I pi R2 is the
magnetic moment of the solenoid divided by its length.
9. Due in recitation 04/17
Go to Hints
Go to Answers
Chapter 31. Induction and Inductance:
46. HRW p. 779 # 25: A rectangular coil of N turns and of
length a and width b is rotated at frequency
f = omega/(2 pi) in a uniform magnetic field
B, as indicated in Figure 31-50 in the text. The
coil is connected to co-rotating cylinders, against which metal
brushes slide to make contact. (a) Show that the emf induced in the
coil is given (as a function of time t) by
EMF = 2 pi f N a b B sin(2 pi f t) = EMF0 sin (2 pi f t).
This is the priciple of the commercial alternating-current
generator. (b) Design a loop that will produce an emf of 150 V when
rotated at 60.0 rev/s in a magnetic field of 0.500 T.
47. HRW p. 780 # 29: A rectangular loop of wire with
length a, width b, and resistance R is
placed near an infinitely long wire carrying current i, as
shown in Fig. 31-53 of the text. The distance from the long wire to
the center of the loop is r. Find (a) the magnitude of the
magnetic flux through the loop and (b) the current in the loop as it
moves away from the long wire with speed v. [Neglect the
magnetic field generated by the current in the loop itself. - MVB]
48. HRW p. 781 # 38:
In Fig. 31-57 of the text a conducting rod of mass m,
resistance R, and length L slides without friction
on two long, horizontal, resistanceless rails. A uniform vertical
magnetic field B fills the region in which the rod is
free to move. The generator G supplies a constant current i
directed as shown in the figure. (a) Find the velocity of the rod as a
function of time, assuming it to be at rest at t = 0. The
generator is now replaced by a battery that supplies a constant
EMF. (b) Show that the velocity of the rod now approaches a constant
terminal value v and give its magnitude and direction. (c)
What is the current in the rod when this terminal velocity is reached?
(d) Analyze this situation and that with the generator from the point
of view of energy transfers.
49. A long solenoid has
n turns per unit length and carries a current given by
I = I0 sin (omega t). The solenoid
has a circular cross section of radius R. Find the induced
electric field at a radius r from the axis of the solenoid
for (a) r < R and (b) r > R.
10. Due in recitation 04/24
Go to Hints
Go to Answers
Chapter 31. Induction and Inductance:
50. HRW p. 782 # 57: Two inductors L1 and
L2 and connected in parallel and separated by a large
distance. (a) Show that the equivalent inductance is given by
1/Leq = 1/L1 + 1/L2.
(Hint: Review the derivations for resistors in parallel and
capacitors in parallel. Which is similar here?) (b) Why must their
separation be large for this relationship to hold? (c) What is the
generalization of (a) for N inductors in parallel?
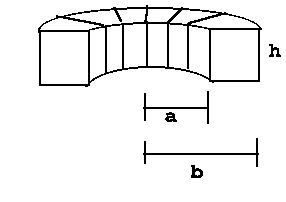 51. Show that the
inductance of a toroid of rectangular cross section, half of which is
shown in the figure, is given by
51. Show that the
inductance of a toroid of rectangular cross section, half of which is
shown in the figure, is given by
L = mu0 N2 h ln(b/a) / (2 pi)
where N is the total number of turns, a is the
inside radius of the toroid, b is its outside radius, and
h is its height.
52. HRW p. 783 # 69. In figure 31-65 of the text,
E = 100 V, R1 = 10.0 Ohms,
R2 = 20 Ohms,
R3 = 30 Ohms, and
L = 2.00 H. Find the values of i1 and
i2 (a) immediately after the closing of switch S, (b) a
long time later, (c) immediately after the reopening of switch S, and
(d) a long time after the reopening.
 53.
For the circuit in the figure, (a) find the rate of change of current
in each inductor and in the resistor just after the switch is
closed. (b) What is the current through the resistor after a long time
has passed?
53.
For the circuit in the figure, (a) find the rate of change of current
in each inductor and in the resistor just after the switch is
closed. (b) What is the current through the resistor after a long time
has passed?

54. In the circuit in the
figure, the switch is closed at t = 0. From time
t to time L/R, find (a) the total energy that has
been supplied by the battery, (b) the total energy that has been
dissipated in the resistor, and (c) the energy that has been stored
in the inductor. Hint: Find the rates as functions of time
and integrate from t = 0 to
t = L/R
11. Due in recitation 05/01
Go to Hints
Go to Answers
Chapter 33. AC Circuits
55. Sketch as a function
of frequency the magnitude of the total impedance Z for (a) a
series LR circuit, (b) a series RC circuit, and (c) and a series LRC
circuit.
56. A resistance
R and a 1.4-H inductance are in series across a 60-Hz AC
voltage. The voltage across the resistor is 30 V and the voltage
across the inductor is 40 V. (a) What is the value of the resistance?
(b) What is the AC input voltage?
57. A coil draws 15 A
when connected to a 220-V AC 60-Hz line. When it is in series with a
4-ohm resistor and the combination is connected to a 100-V battery,
the battery current after a long time is observed to be 10 A. (a)
What is the resistance in the coil? (b) What is the inductance of the
coil?
12. Due in recitation 05/08
Go to Hints
Go to Answers
Chapter 33. AC Circuits:
58. HRW p. 839 # 85 (Compare figure 33-35): A series
LRC circuit has R = 15.0 ohms,
C = 470 microfarads, and L = 25.0 mH.
The generator driving the circuit provides a sinusoidal voltage of
75.0 V (rms) and frequency f = 550 Hz. (a)
Calculate the rms current. (b) Find the rms voltages across the
resistor, the capacitor, the inductor, the capacitor and inductor
together, and across the resistor, inductor, and capacitor together.
(c) At what average rate is energy dissipated by each of the three
circuit elements?
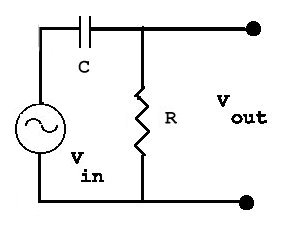 59. The circuit shown in
the figure is called an RC high-pass filter because high input
frequencies are transmitted with greater amplitude than low input
frequencies. (a) If the input voltage is
59. The circuit shown in
the figure is called an RC high-pass filter because high input
frequencies are transmitted with greater amplitude than low input
frequencies. (a) If the input voltage is
Vin = V0 cos(omega t),
show that the output voltage [the potential difference between the two
black dots in the figure] is
V0 cos (omega t + phi)
Vout = -------------------------
[ 1 + (omega R C)-2 ]1/2
and determine the value of phi. (b) At what angular
frequency is the output voltage half the input voltage? (c) Sketch a
graph of the amplitude of Vout/V0 as a function
of omega.
60. A resistor and an
ideal inductor are connected in parallel across an emf
V = V0 cos(omega t). Show that
(a) the current in the resistor is
IR = (V0/R) cos(omega t),
(b) the current in the inductor is
IL = (V0/XL)cos(omega t - pi / 2),
(c) I = IR + IL
= Imaxcos(omega t - delta) where
tan(delta) = R/XL and
Imax = V0/Z with
Z -2 = R -2 + XL -2.
61. Solve for the amplitudes of all the currents in a
circuit which has a capacitor in series with a parallel combination of
a resistor and an ideal inductor. Use the values R=10 ohms,
|XL|=30 ohms, |XC|=10 ohms, and
|V0|=20 volts.
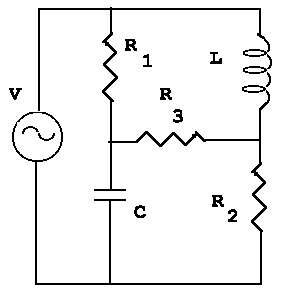 62. Find the amplitudes of all the currents in the
3-loop circuit in the figure. Use
R1 = 10 ohms,
R2 = 40 ohms,
R3 = 20 ohms,
XL = 30 ohms,
XC = 10 ohms, and
V = 15 Volts. Do the calculation numerically or use a
computer-algebra program to work the problem analytically.
62. Find the amplitudes of all the currents in the
3-loop circuit in the figure. Use
R1 = 10 ohms,
R2 = 40 ohms,
R3 = 20 ohms,
XL = 30 ohms,
XC = 10 ohms, and
V = 15 Volts. Do the calculation numerically or use a
computer-algebra program to work the problem analytically.
 2. Four charges,
each of magnitude q, are at the corners of a square of side
L. The two charges at one pair of opposite corners are
positive, and the other two charges are negative. Find the force
exerted on either of the negative charges by the three remaining
charges. See figure to the right.
2. Four charges,
each of magnitude q, are at the corners of a square of side
L. The two charges at one pair of opposite corners are
positive, and the other two charges are negative. Find the force
exerted on either of the negative charges by the three remaining
charges. See figure to the right.




 12. A spherical shell
of radius R carries a uniform surface charge density
sigma which you may consider to be positive. The figure to
the right shows a cross-section of the shell. A point P is
in the plane of the cross-section but not at the center. Consider the
two elements of the shell of areas s1 and
s2 shown in the figure at distances
r1 and r2 , respectively, from
point P. (a) Show that the ratio of the charges on these
elements is
Q1 / Q2 = r1 2 / r2 2
(b) Which produces the greater field at point P? (c) What is
the direction of the field at point P due to each element?
What is the direction of the total electric field at point P?
(d) Using the result in part (c), explain how it is possible to use
Gauss's Law to calculate the electric field without taking into
account any charges outside the Gaussian surface, provided that
sufficient symmetry is present. What is the role of the symmetry
requirement?
12. A spherical shell
of radius R carries a uniform surface charge density
sigma which you may consider to be positive. The figure to
the right shows a cross-section of the shell. A point P is
in the plane of the cross-section but not at the center. Consider the
two elements of the shell of areas s1 and
s2 shown in the figure at distances
r1 and r2 , respectively, from
point P. (a) Show that the ratio of the charges on these
elements is
Q1 / Q2 = r1 2 / r2 2
(b) Which produces the greater field at point P? (c) What is
the direction of the field at point P due to each element?
What is the direction of the total electric field at point P?
(d) Using the result in part (c), explain how it is possible to use
Gauss's Law to calculate the electric field without taking into
account any charges outside the Gaussian surface, provided that
sufficient symmetry is present. What is the role of the symmetry
requirement?












