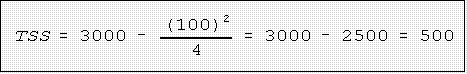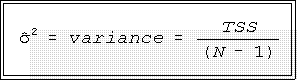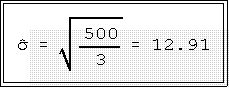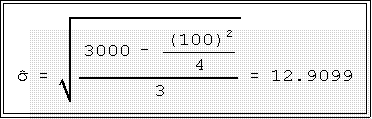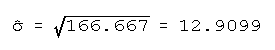DEPARTMENT OF POLITICAL SCIENCE
AND
INTERNATIONAL RELATIONS
Posc/Uapp 815
Descriptive Statistics
(Continued)

- CLASS 7 AGENDA:
- Interpretation of hinges
- The arithmetic mean
- The standard deviation and variance, measures of dispersion
- Summation notation
- Reading:
- Agresti and Finlay, Statistical Methods, pages 45 to 67. (Look for the
topics we're covering.)
- INTERPRETATION OF DISPLAYS AND ORDER STATISTICS:
- The stem-and-leaf display is
analogous to frequency distributions and histograms
described in most basic statistics texts,
but is easier to calculate and draw. It also
simplifies the computation of other exploratory statistics.
- The interpretation of the hinge:
- See Figure 1. 50 percent
of the cases (states) lie between 280 BTUs per
capita and 380 BTUs. Note that the hinges scores are not equally distant
from the median.
- What interpretation can we put on these numbers? The median is fairly self-explanatory in this case. It represents the middle or typical value in that
some states have lower, some higher per capita rates of energy
consumption.
- Now look at the variation. Lets look at the "middle" 50 percent of states,
the ones between the hinges, which are 280 and 380. So apparently there is
not much variation in energy consumption among the middle group of
states. After all, the difference is only 100 BTUs. Moreover, we see from
the stem-and-leaf display that most values are within few hundred BTUs of
average. Only a few states have relatively high rates of consumption.
- An important task might be to identify those places and decide why
they are considerably above average.
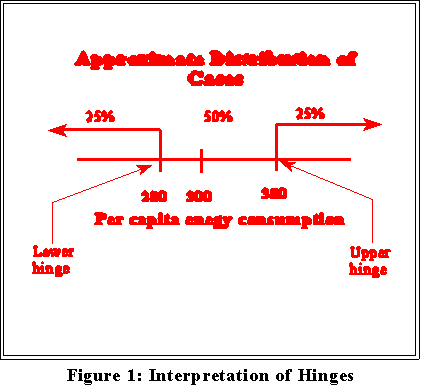
- We can contrast this "amount" of variation with a situations where
there is much more or much less, just to see how hinges might be
used to assess differences.
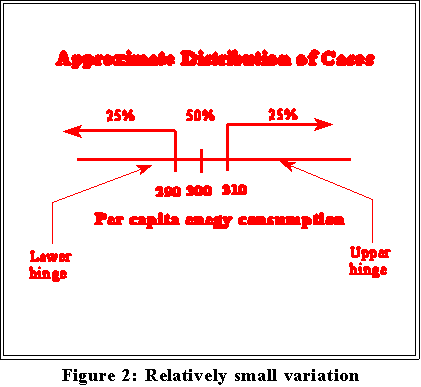
- Figure 2 shows limited variation: 50 percent of the states lie between 290
and 310 BTUs. In Figure 3, by contrast there is much more variation
because the middle 50 percent of cases extend from 300 to 480.
- In moment we will add maximum and minimum values to create a
"boxplot" that presents and even clearer view of variation.
- A key question is: why is there such great variation? As I mentioned in the
previous class, part of the explanation may lie in cross-national differences
in attitudes and approaches to illness and health care.
- What MINITAB does:
- MINITAB stem-and-leaf displays will not look like yours (usually) but the
letter values should be the same, except that MINITAB calculates more of
them.
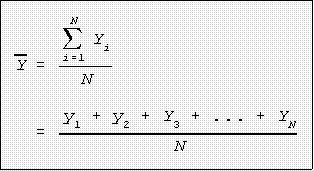
- THE MEAN:
- To repeat what was said in an earlier class, the mean is the sum of all values in the
batch or sample divided by the total number, N, of values
- Formula for a batch of numbers or sample:
- Symbol for the sample or
observed mean is
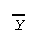 ,
which is read "Y bar." For a
population (see later) the mean is
denoted with the lower case greek letter mu, .
,
which is read "Y bar." For a
population (see later) the mean is
denoted with the lower case greek letter mu, .
- Summation: The summation symbol, sigma, means addition In particular, it tells
you what and how to add.
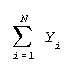 means add Y1, Y2, and so forth until the last data value (the Nth)
is reached.
means add Y1, Y2, and so forth until the last data value (the Nth)
is reached.- Here is an example.
Suppose we have 5 numbers: 10 20 30 40 50.
- The summation symbol

means let add the first observation (i = 1), then the second (i = 2), then the
third (1 = 3) and so on
until i = 5 so stop adding with the fifth number.
- This quantity is called the sum of the Ys.
In the example, this sum is
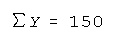 .
.
- Properties of the mean:
- The sum of the deviations from the mean are zero.
- In other words, find the mean,
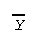 ,
then subtract
,
then subtract
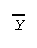 from each
number, and add these "deviations." The total will be 0. Example:
from each
number, and add these "deviations." The total will be 0. Example:
Data: 10 20 30 40 50
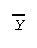 = 30
= 30
Deviations are (10 - 30) = -20, (20 - 30) = -10...
Sum of deviations is (-20) + (-10) + (0) + (10) + (20)
= 0
- In this instance, the sum of squared Ys or sum of squares for
short is:
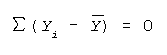
- The sum of all squared deviation is a minimum. In other words, suppose
we square all of the deviations above (e.g., (-20)2, (-10)2, etc.) and then
add these squares. The sum will be a positive number but it will be at least
as small and probably smaller than if we had used some other number
besides the mean.
- Example:
Data: 5 10 15 70
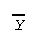 = 25
= 25
Median (M) = 12.5 (why?)
Squared deviations from
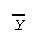 :
Squared deviation from M:
:
Squared deviation from M:

- Notice that when deviations are taken from the mean they are
smaller than when taken from the median.
- As noted in an earlier class, the mean is sensitive to extremely larger or
small values. This is a reason why, for example, many studies and
government reports use median rather than mean income.
- MEASURES OF DISPERSION:
- Variation: the total variation in a batch of numbers equals the sum of the squared
deviations about the mean.
- The total variation is also called the total sum of squares.
- Its formula is:
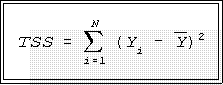
- In words: for a batch of numbers find the mean,
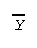 ,
then subtract it from
the first data point and square the difference.
Do the same for the second
observation, the third and so on. When done add up these squared
differences.
,
then subtract it from
the first data point and square the difference.
Do the same for the second
observation, the third and so on. When done add up these squared
differences.
- Example: 10 20 30 40

- That is,
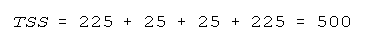
- Computing formula:
- When you have lots of data, the total sum of squares can be calculated
easily with a good calculator by finding the sum of the Ys' and the sum of
the Y's squared; that is:

- Then put these quantities in this formula, called a computing formula:

- Example:
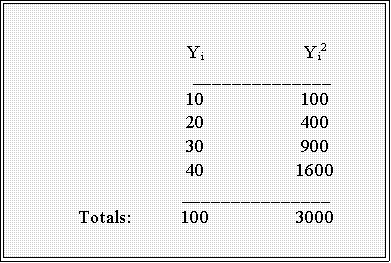
- The total sum of squares is thus:
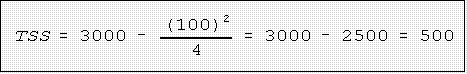
- Variance:
- The variance of a batch of numbers or sample is denoted
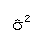 ,
for a batch
of numbers and represents the total
variation divided by N minus 1:
,
for a batch
of numbers and represents the total
variation divided by N minus 1:
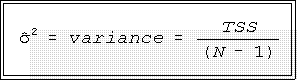
- Example: 10 20 30 40
- As seen above the TSS is 500.
Therefore the variance of this batch
of numbers is:

- The larger the variance, the more variation or
dispersion in the data. But it
is difficult to give an intuitive interpretation to any particular value such as
500.
- The Standard deviation:
- The standard deviation of a batch of numbers or sample,
denoted
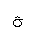 is
(loosely speaking) the average of the
squared deviations from the mean.
Since deviations indicate how much variation exists in the data,
having an
average of these differences tells one about overall variation.
is
(loosely speaking) the average of the
squared deviations from the mean.
Since deviations indicate how much variation exists in the data,
having an
average of these differences tells one about overall variation.
- It is also the square root of the variance.
- To calculate the standard
deviation, therefore, first obtain the total
sum of squares by summing the
squared deviations from the mean:

- Then divided this total by N - 1, where N is the number of cases in
the batch.
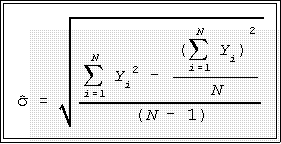
- Finally, take the square root:
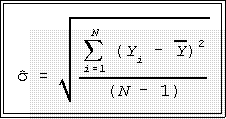
- Example: 10 20 30 40; mean = 25

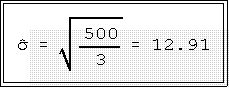
- Computing formula:
- As be expected, since it is just the square of the total sum of
squares divided by N minus 1, the standard deviation can be
calculated easily with a good calculator by finding the sum of the
Ys' and the sum of the Y's squared; that is (as before):

- Put these quantities in the computing formula:
- In the previous example, the sum of the Y's squared was 3000 and
the sum of the Y's alone was 100 so:
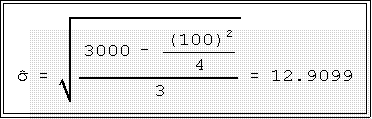
- A simpler way to get this
number of course is to simply take the
square root of the variance which we found above to be 166.667:
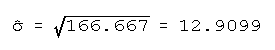
- Interpretation:
- The larger the standard deviation,
the greater the variation in a batch of
numbers, other things being equal.
- MINITAB AND STATISTICAL CALCULATIONS (OPTIONAL):
- The descriptive statistics menu gives the mean and standard deviation.
- You can also use the commands mean (e.g., mean c2) and standard (e.g.,
standard c7) in the session window.
- You can also use MINITAB as a pocket calculator. Doing so, in fact, enhances
your understanding of both statistical computations (e.g., the summation sign) and
MINITAB itself.
- In the student version open menu Calc and then Mathematical
expressions.
- In the box you can type in an
expression composed of columns and
commands.
- In the standard or full version use
Calculator option on the
Calc menu.
- We'll see some example in class.
- NEXT TIME:
- More descriptive statistics
- Histograms and cumulative frequency distributions.

 Go to Statistics main page
Go to Statistics main page
 Go
to H. T. Reynolds page.
Go
to H. T. Reynolds page.
Copyright © 1997 H. T. Reynolds




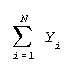 means add Y1, Y2, and so forth until the last data value (the Nth)
is reached.
means add Y1, Y2, and so forth until the last data value (the Nth)
is reached.
![]() = 30
= 30
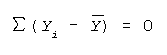
![]() = 25
= 25
![]() :
Squared deviation from M:
:
Squared deviation from M:



![]()